コルモゴロフ–スミルノフ検定（コルモゴロフ–スミルノフけんてい、英: Kolmogorov–Smirnov test）は統計学における仮説検定の一種であり、有限個の標本に基づいて、二つの母集団の確率分布が異なるものであるかどうか、あるいは母集団の確率分布が帰無仮説で提示された分布と異なっているかどうかを調べるために用いられる。しばしばKS検定と略される。

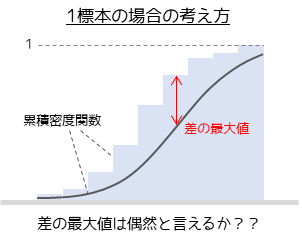
1標本KS検定は、経験分布を帰無仮説において示された累積分布関数と比較する。主な応用は、正規分布および一様分布に関する適合度検定である。正規分布に関する検定については、リリフォースによる若干の改良が知られている（リリフォース検定）。正規分布の場合、一般にはリリフォース検定よりもシャピロ-ウィルク検定やアンダーソン-ダーリング検定の方がより強力な手法である。

2標本KS検定は、二つの標本を比較する最も有効かつ一般的なノンパラメトリック手法の一つである。これは、この手法が二つの標本に関する経験分布の位置および形状の双方に依存するためである。

検定統計量

n個の標本y1, y2, ..., ynに対する経験分布Fnは以下のように与えられる。

F n ( x ) = # { 1 ≤ i ≤ n ∣ y i ≤ x } n {\displaystyle F_{n}(x)={\frac {\#\{\,1\leq i\leq n\mid y_{i}\leq x\,\}}{n}}}

このとき F(x) を帰無仮説で提示される分布、またはもう一方の経験分布とすると、二つの片側KS検定統計量は、以下で与えられる。

D n = sup x ( F n ( x ) − F ( x ) ) {\displaystyle D_{n}^{ }=\sup _{x}(F_{n}(x)-F(x))}
D n − = sup x ( F ( x ) − F n ( x ) ) {\displaystyle D_{n}^{-}=\sup _{x}(F(x)-F_{n}(x))}

二つの分布が等しいという帰無仮説が棄却されないと仮定する場合、上記の二つの統計量が従うべき確率分布は、仮説で提示される分布が連続分布である限りにおいて、分布の形に依存しない。

クヌースはこの1対の統計量に関する有意性を解析する方法に関する詳細な記述を与えている。多くの人々は2つの統計量の代わりに

D n = sup x | F n ( x ) − F ( x ) | = max ( D n , D n − ) {\displaystyle D_{n}=\sup _{x}\vert F_{n}(x)-F(x)\vert =\max(D_{n}^{ },D_{n}^{-})}

という統計量を用いるが、この統計量の分布はさらに扱いにくい。

有意確率

1標本KS検定では、サンプルサイズnが十分大きいとき、経験分布Fn(x)が帰無仮説に従う（すなわち、経験分布が帰無仮説で提示された分布F(x)と一致する）と仮定した下での場合の検定量の分布は

Prob ⁡ ( n D n ≤ x ) = 1 − 2 ∑ i = 1 ∞ ( − 1 ) i − 1 e − 2 i 2 x 2 = 2 π x ∑ i = 1 ∞ e − ( 2 i − 1 ) 2 π 2 / ( 8 x 2 ) {\displaystyle \operatorname {Prob} ({\sqrt {n}}D_{n}\leq x)=1-2\sum _{i=1}^{\infty }(-1)^{i-1}e^{-2i^{2}x^{2}}={\frac {\sqrt {2\pi }}{x}}\sum _{i=1}^{\infty }e^{-(2i-1)^{2}\pi ^{2}/(8x^{2})}}

で与えられる。したがって、有意水準を α {\displaystyle \alpha } とするとき、検定量Dnが n D n > K α {\displaystyle {\sqrt {n}}D_{n}>K_{\alpha }} （ただし K α {\displaystyle K_{\alpha }} は Prob ⁡ ( n D n ≤ K α ) = 1 − α . {\displaystyle \operatorname {Prob} ({\sqrt {n}}D_{n}\leq K_{\alpha })=1-\alpha .\,} を満たす数）を満たすとき、帰無仮説は棄却され、経験分布Fn(x)は帰無仮説で提示された分布F(x)とは異なることが示唆される。

その他

1年のうちの1日や、あるいは1週間のうちの1日といったように、独立変数が周期性を持つ場合、カイパー検定の方がより適切である。数値解析の有名な著作である"Numerical Recipes"には、このことに関する詳しい情報が記載されている。

さらに、コルモゴロフ-スミルノフ検定は分布の裾の部分よりも中央値付近の方に強く依存する。これに対して、アンダーソン-ダーリング検定は裾でも中央値付近でも等しい感度を与える。

脚注

参考文献

  • William H.Press, William T. Vetterling, Saul A. Teukolsky, Brian P. Flannery 著、丹慶勝市・奥村晴彦・佐藤俊郎・小林誠 訳『ニューメリカルレシピ・イン・シー日本語版―C言語による数値計算のレシピ』（1版）技術評論社、1993年。ISBN 978-4874085608。 
  • Durbin, J. (1973). Distribution theory for tests based on the sample distribution function. Society for Industrial and Applied Mathematics. ISBN 978-0-89871-007-6. MR0305507. https://books.google.co.jp/books?id=zAryCrT1IUYC 

関連項目

  • アンドレイ・コルモゴロフ
  • リリフォース検定
  • シャピロ-ウィルク検定
  • アンダーソン-ダーリング検定
  • ジャック-ベラ検定

外部リンク

  • 分位数の表 — Pestman, Wiebe R. (2009). Mathematical statistics. de Gruyter Textbook (Second ed.). Walter de Gruyter. ISBN 978-3-11-020852-8. MR2516478. Zbl 1251.62001. https://books.google.co.jp/books?id=9QHcJ8WQQ5UC 

【徹底解説】コルゴモロフ・スミルノフ検定｜Staat

【徹底解説】コルゴモロフ・スミルノフ検定｜Staat

El criterio de homogeneidad de Smirnov como indicador de la no

2標本コルモゴロフスミルノフ検定を試す 分析ノート

コルモゴロフスミルノフ検定